Smoothing images with the Mumford Shah functional

My python implementation for minimizing the Mumford Shah functional.

    import cv2
    from AmbrosioTortorelliMinimizer import *

    img = cv2.imread("image.jpg", 0)
    solver = AmbrosioTortorelliMinimizer(img)
    img, edges = solver.minimize()

The Mumford Shah functional, one of the most cited models in Computer Vision,
is designed to smooth homogeneous regions in an image, while enhancing edges.
You can minimize it to get edge preserving smoothing, or a segmentation of the image, depending on the parameters you choose.

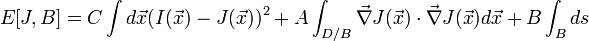
The functional tries to enforce some conditions on the target image J:
1. The target image J should be similar to the input image I.
2. The target image J should be smooth, except at a set of edges B.
3. There should be few edges.

That’s a hard optimization problem.
Luckily, Ambrosio and Tortorelli showed that the functional can be represented in terms of another functional, where the edge set B is modeled by multiplication with a continuous function that represents the edges, and converges to the original mumford-shah functional when ɛ approaches 0.

z is ~0 for edges, and ~1 for smooth pixels.
The optimization problem is now to minimize:

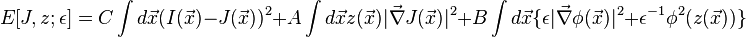
Using functional calculus you can take derivatives of that, and obtain a linear system of equations for solving:
1. The edge set Z.
2. The image J.
Both depend on one another, so usually an alternation scheme is used:
Solve for the edge set Z while fixing J, and then solve for J while fixing Z.
To derive the equations I followed http://www.eng.tau.ac.il/~nk/TRs/LeahTIP2006.pdf
That paper also shows you can use the same functional as a regularizer for reconstructing sharp images out of blurred ones if you have the blurring kernel, or if you parameterize the kernel as a Gaussian.

There are a few practical problems with all this, though:

1. Solving such a huge set of equations (one equation for every pixel) is slow.
   I provided the conjugate gradient solver a linear operator, instead of creating and storing a huge matrix.
   I wonder if using a pre-conditioner would do any good for speed of convergence.
   Also there should probably be a unified calculation for RGB images, instead of smoothing each channel.
2. You have to choose a good value of ɛ.

In my implementation for the purpose of speed I set the default parameters to be few iterations and a high numerical tolerance. Results look good for even one AM iteration.
It’s pretty straight forward to implement on a GPU, since single pixel calculations are independent of one another.
On my machine the unconcurrent python implementation run time for 640x480 color images was about 0.6 seconds, so I guess a GPU implementation would speed it up a lot.
There is lots of ongoing work on phrasing other minimization problems to solve the same thing, and it’s getting close to real time.
In this paper (github repo) they phrased a similar functional, that’s independent of ɛ or the edge set (they model the edge set in terms of the image gradient), and boast 20 fps performance for color images.
They did use a GPU implementation, and a strong GPU to achieve that,
so I wonder what would be the performance of a GPU implementation for the Ambrosio-Tortorelli minimization.